When using mercury intrusion porosimetry data, due to the high pressures used during the experiment (up to 414 MPa) and the differing compressibilities of mercury, sample and penetrometer, the results are subject to various compressibility errors and these need to be corrected to obtain a true measure of the void space of a sample.
If the sample was completely incompressible, the experimentally observed mercury intruded volume, Vobs, would include the volume of mercury intruded into the sample, Vint, the volume expansion of the analysis chamber or penetrometer, δVpen, and the compression of the mercury δVHg (Gane et al., 1996):
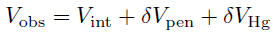
[1]
The term representing the expansion of the chamber can be evaluated by running a blank run with no sample in the penetrometer. The term representing the compressibility of the mercury itself can be evaluated by using experimentally derived equations, which relate the volumetric compression of mercury as a function of pressure. The working equation for an incompressible sample becomes:
![]()
[2]
where δVblank is the change in the blank run volume reading, V1bulk the sample bulk volume at atmospheric pressure and Papp the applied external pressure in MPa.
In order to obtain a correct interpretation of the mercury porosimetry intrusion curves one has to take into account this compressibility and apply another correction to the observed intruded volume. If Ψss is the compressibility of the sample and Mss its bulk modulus, then
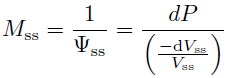
[3]
The final expression for the fully corrected intruded volume is shown in Equation 4. The raw mercury intrusion curves can be corrected for these errors using the Porexpert compressibility correction algorithm.
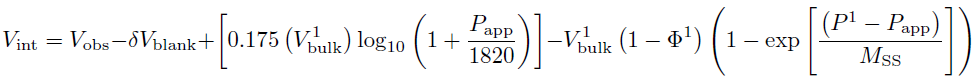
[4]
where Φ1 is the porosity of the sample at one atmosphere, P1 is the atmospheric pressure.
Further reading into the derivation of Equation 4, may be found in Gane et al., 1996, and gives a comprehensive insight into how the correction procedure is used to provide true volumes of intrusion for a sample. The equation also allows calculation of the bulk modulus of the sample, which refers to a ratio of applied pressure to the decrease in sample volume when a uniform pressure is applied to the surface of a material. The bulk modulus is the inverse of compressibility and is given in units of pressure. Large values of bulk modulus imply the sample is relatively incompressible and those with small values highly compressible. For comparison polystyrene has a bulk modulus of around 3.5 GPa and diamond has a bulk modulus of around 440 GPa.