The PoreXpert algorithm is based on that published by Laudone et al., with an improvement for fluid tortuosity. The algorithm measures the ratio between the length of the most likely path of an ion moving through the simulated void structure from super-source to super-sink, relative to the distance between the parallel planes of the super-source and super-sink. The super-source is an infinite plane at z = h, where h is the unit cell size, supplying ions or fluid in the direction shown here, and the super-sink is a parallel infinite plane at z=0. These planes are at the top and bottom of the unit cell, for example as shown in the description of unit cell structure types.
Each pore of the simulated void network, including the source and the sink, can be schematically represented as a node of a network graph, which has the interconnecting throats as edges. The statistical weight of each pore-throat-pore arc is unity, and Yen's algorithm and Dijkstra shortest path algorithm are used to evaluate the 100 shortest paths between source and sink. This is repeated 5 nz times, where nz is the number of nodes in the direction of the z axis. In order to force the algorithm to explore longer and more tortuous paths, a number of throats, proportional to the total number of features in the unit cell and larger at each of the 5 nz iterations, is discounted from the graph. Finally, duplicates are removed from the list of 500 nz paths and the total resistance of each path is calculated as a sum of the resistances of each pore-throat-pore arc.
Ionic tortuosity. The distance from the centre of a cubic pore to the centre of an adjoining throat is lp / 2 , where lp is the side length of the pore, so the electrical resistance of this section of the arc is proportional to this distance divided by the cross-section, i.e. lp / 2 l2p. The electrical resistance Rα-β of the whole arc between two nodes α and β connected by a cylindrical throat of length lt and radius rt, is:
![]()
where ρ is the resistivity of the arc.
Fluid tortuosity. For liquids and dense gases that do not exhibit Knudsen flow because of their density or because of the relatively large size of the voids through which they are passing (typically > 1 μm), the Poiseuillian flow resistance can be calculated by parameterising the relevant Navier Stokes equations (Matthews et al., 2006):
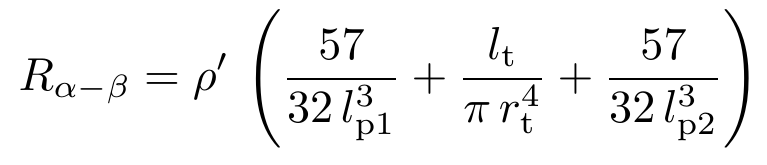
For an entire path of length n arcs from source (α = 0) to sink (β = n) there is a maximum displacement distance δx,y in the xy plane normal to the perfectly direct path of nz arcs in the z direction, given by Pythagoras as δx,y = √(n2-nz2). Assuming that the choice of route by an ion at node α is Markovian, then the probability of choice of route will depend simply on the reciprocal of the apparent resistance of each arc connected to that node. Therefore the probability ψn of an ion going through a path which is n arcs long and with a value of resistance R0-n is inversely proportional both to the average resistance of the pathway R0 - n / n, and to δx,y:
![]()
The total probability Ψn of an ion going through any path within the ensemble of paths of length n arcs is the sum of all the individual path probabilities:
![]()
The algorithm finds the length neff, expressed as a number of arcs, of the path with value of the probability equal to the median value of the distribution of Ψn, and it calculates the value of tortuosity as:
![]()